The Fascinating World of Microorganisms
The genesis for this exploration came after watching Journey to the Microcosmos on YouTube, a channel that delves deep into the world of microscopic organisms, many of which were discovered in Poland. At first glance, one might dismiss microscopic organisms as mundane - after all, how interesting can amoeba really be? What do they do beyond swimming around and ingesting plant particles?
Yet, this simplistic view mirrors our potential misconception of any natural creature featured on BBC's Planet Earth. While their basic function might be survival through consumption, the complexity and diversity in how they achieve this is remarkable.

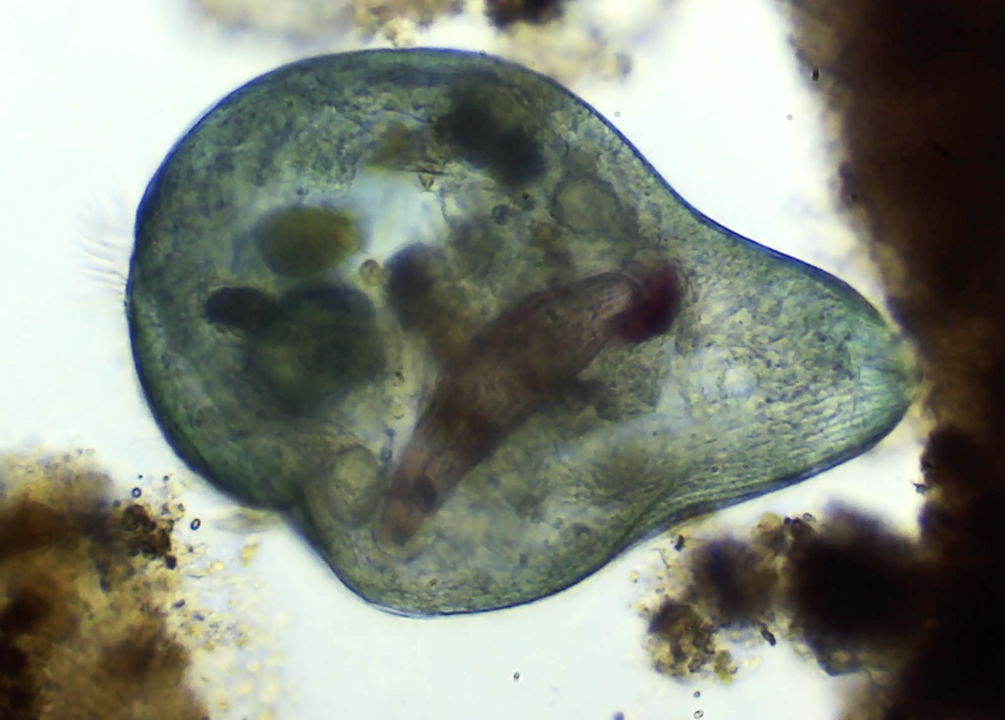
Complexity in Simplicity
What's particularly striking is the complexity that emerges from these tiny organisms. Despite their limited scope of action, microorganisms display incredible variation in their survival strategies. Some are filter feeders, others aggressive predators. Some produce powerful neurotoxins, while others have achieved functional immortality.
Microscopic organisms may be small, but their survival strategies are anything but simple. Despite their tiny size, these life forms have evolved an astonishing array of behaviors—from delicate filter feeding to aggressive predation—that enable them to thrive in diverse environments. Equally impressive is their biochemical arsenal. Some microbes produce potent neurotoxins, not only as a means of defense but also to secure their next meal. Every unclassified strain represents a unique evolutionary experiment, where random mutations lead either to flourishing new traits or eventual extinction. Moreover, these organisms form intricate communities, sharing genetic material and coordinating survival strategies. This interplay not only enhances their resilience but also offers promising insights for breakthroughs in medicine and environmental science. In essence, even the smallest corners of our biosphere are filled with remarkable complexity, proving that size doesn’t limit ingenuity.
Modeling Ecosystem Stability
This raises an intriguing question: what maintains stability in such complex systems? How do various classes of entities coexist, and what happens when we alter the physical pressures in their environment?
From first principles, one might expect a successful ecosystem to display sinusoidal behavior, where maximum values indicate the point at which each group reaches its sustainability limit and begins to decline.
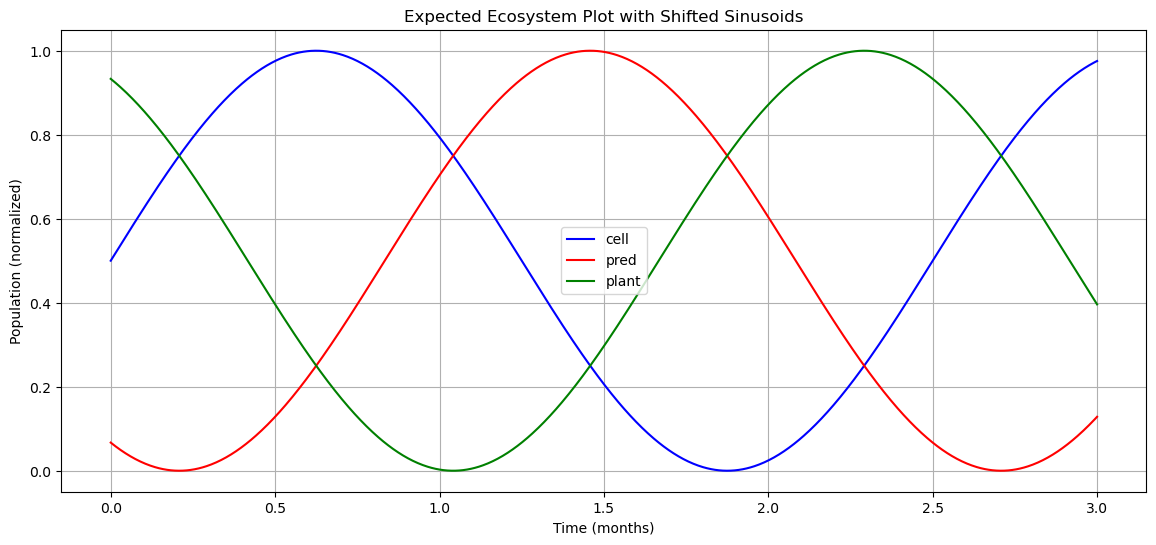
The Kolmogorov Model
The Kolmogorov model, which serves as the foundation for understanding Predator-Prey relationships, confirms this sinusoidal pattern through two key equations:
$$Prey(\frac{dx}{dt}) = ax - bxy$$ $$Predator(\frac{dy}{dt}) = -cy + dxy$$- a represents the natural growth rate of the prey
- b represents the predation rate coefficient
- c represents the natural death rate of predators
- d represents the rate at which predators increase by consuming prey
We can run this model on something basic like 40 prey and 9 predators.
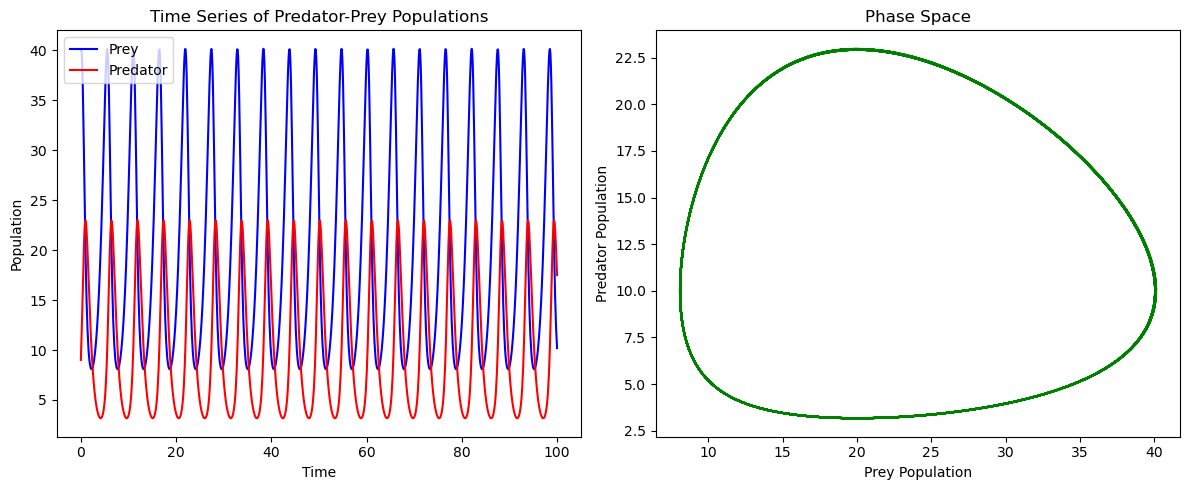
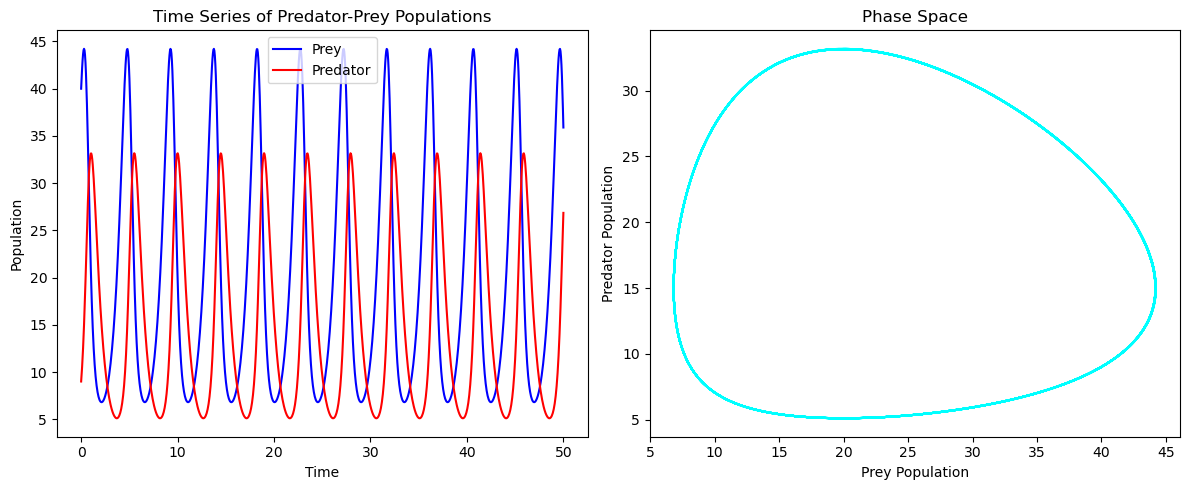
You can see the matching sinusoidal pattern, the peaks are much sharper, but this is an artifact related to the timescales we are selecting. I think we are on the right track. We can see that this is a closed system. When the prey population increases, predators have more food, leading to an increase in the predator population. As the predator population grows, it starts to reduce the prey population, which eventually leads to a decline in predator numbers due to reduced food availability. With fewer predators, the prey population can recover, and the cycle repeats.
This is kind of what I had in my head which made conceptual sense. But it only models systems with a single predator and prey animal. I also wanted to give myself a baseline based on the food that the herbivores are going to eat before thye are turned into prey. We can model this with an additonal equation
$$Plant Food: (\frac{dx}{dt}) = \beta \alpha F x - b x y$$
We are going to build everything in PyGame to get a scaffolding in place which we test out everything. PyGame allows us to prototype the system and get some visual cues about what is happeneing. Once we start running the simulaton in earnest and trying a variety of parameters, it will be computationally expensive to generate live plots for the volume of parameters we want to work with. For now I think it is illustrative. Our tasks for the beginning are:
- Create PyGame window and draw something on the screen
- Create some sprites
- Test growth energy
- Collision detection for consuming plants and cells
- Logging Tasks
- Implement Plotting
- Set respawn distances for cell division
- Brownian motion for the particles
